Olá, amiguinhos curiosos!
Que legal ter vocês aqui no nosso cantinho do saber!
Hoje vamos embarcar juntos numa aventura incrível pelo mundo da Geometria. Preparados para descobrir formas, tamanhos e segredos?
Vocês já repararam como o mundo é cheio de formas? Algumas são retas, outras são curvas… E hoje vamos falar de duas formas muito especiais que parecem primas: a circunferência e o círculo!
Imaginem só:
- Um bambolê que vocês adoram girar na cintura.
- O anel brilhante da mamãe ou do papai.
- O pneu da bicicleta que nos leva para passear.
Todas essas coisas têm a forma de uma circunferência! A circunferência é como o contorno, a “borda” dessas coisas. É só a linha que faz a volta, sem preencher o meio. Pensem num desenho feito com um barbante esticado, que forma uma roda. Isso é uma circunferência! Então, quando a gente vê o contorno de um bambolê, estamos vendo uma circunferência.
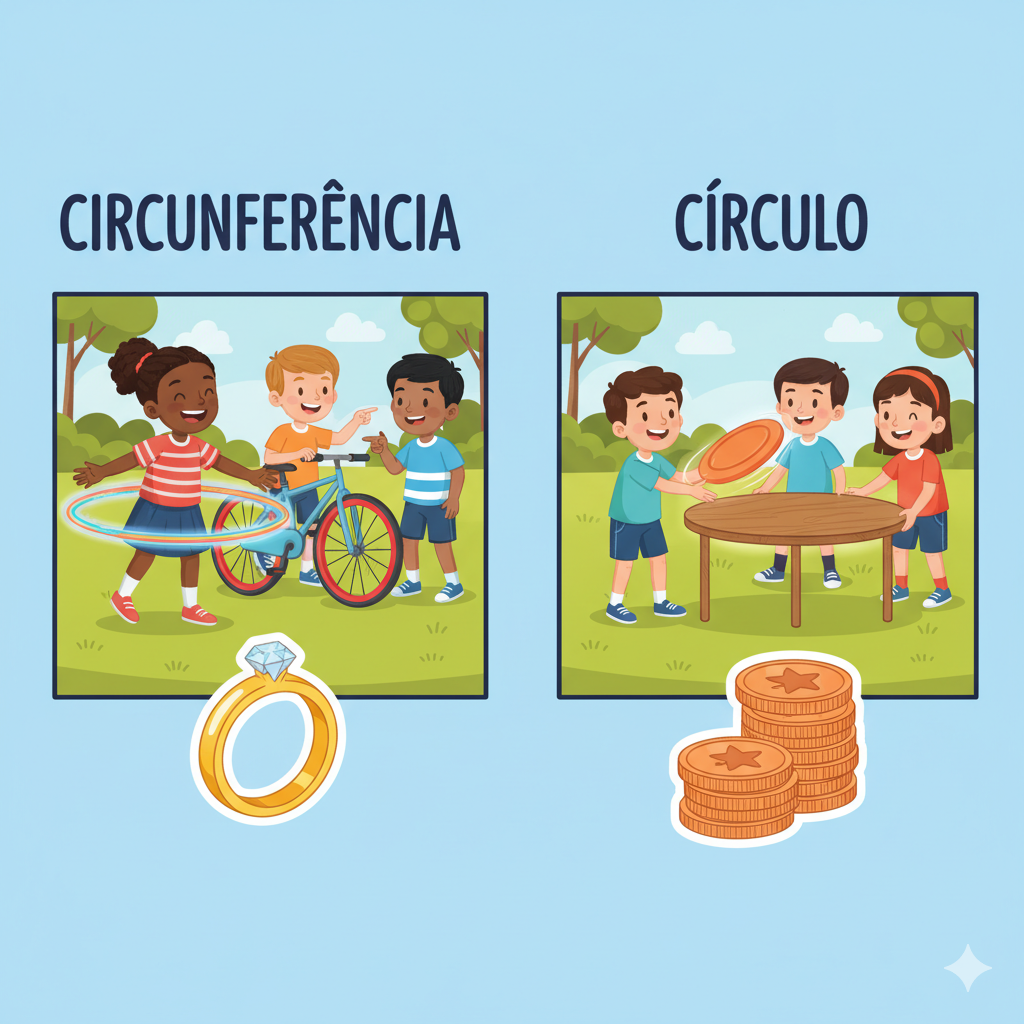
Agora, vamos pensar em outras coisas:
- Um frisbee que a gente joga no parque.
- O tampo redondo da mesa onde fazemos nossas refeições.
- A moeda que usamos para comprar algo gostoso.
Essas coisas são um círculo! O círculo é a circunferência mais o seu interior, ou seja, tudo o que está dentro do contorno. É como se a gente pegasse o bambolê e preenchesse ele todinho por dentro com uma cor. O frisbee, o tampo da mesa e a moeda são exemplos perfeitos de círculos. Viram a diferença? A circunferência é só a borda, e o círculo é a borda com tudo que está dentro!
Desvendando os Segredos da Circunferência
A circunferência, que parece tão simples, tem uns amigos que nos ajudam a entender melhor como ela funciona. Vamos conhecer cada um deles!
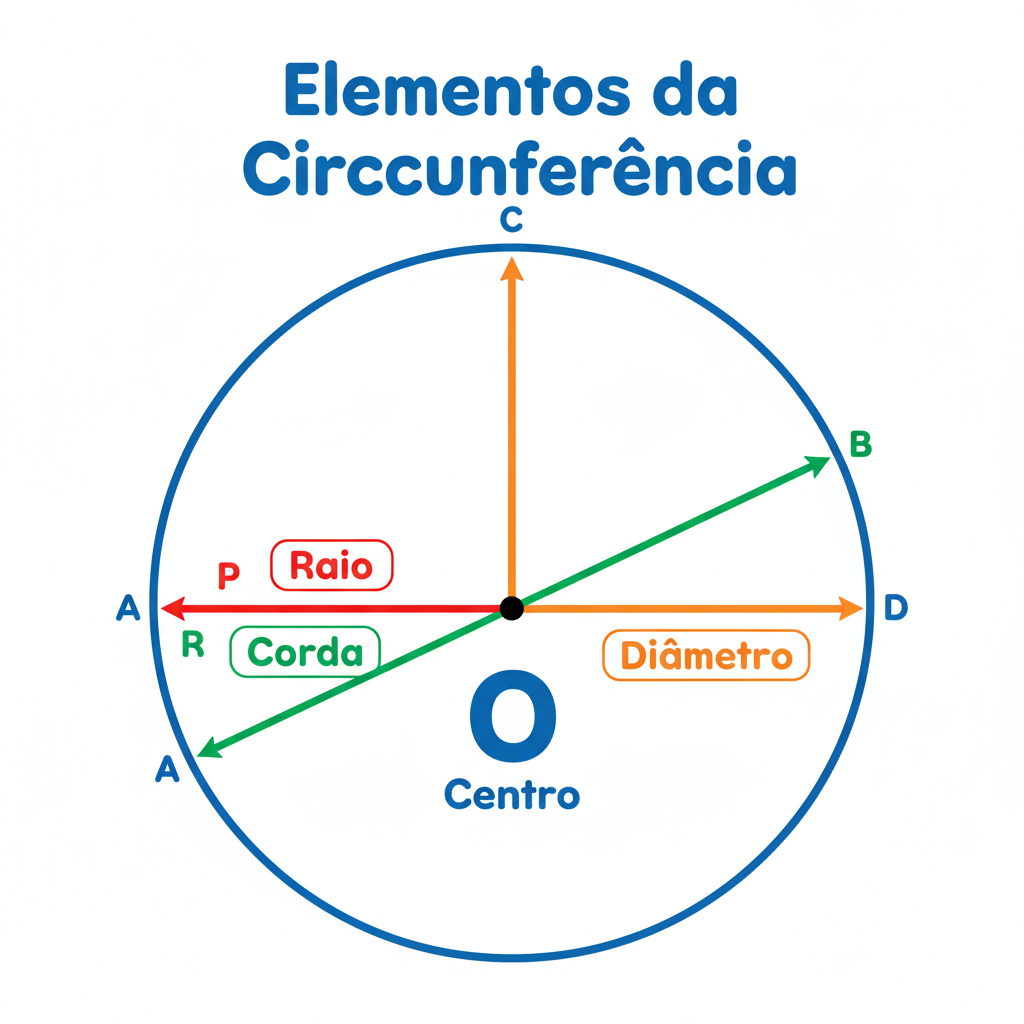
- O (Centro): Imaginem que vocês estão no meio de uma roda gigante. O centro da roda é exatamente o Centro da circunferência! É o ponto que fica bem no meio, à mesma distância de todos os pontos da borda. Ele é muito importante, pois é a partir dele que tudo começa!
- P (Ponto da Circunferência): Qualquer pontinho que esteja na linha da circunferência é chamado de Ponto da Circunferência. Pensem nos pontos que formam o contorno do bambolê.
- R (Raio): O Raio é como uma “ponte” que vai do Centro (O) até qualquer Ponto (P) na circunferência. É sempre a mesma distância, não importa para onde você aponte do centro até a borda! Pensem num raio de sol saindo do meio e indo para fora. Ele nos ajuda a saber o tamanho da circunferência!
- AB (Corda): A Corda é um segmento de reta que liga dois pontos da circunferência, mas não precisa passar pelo Centro. Pensem em um barbante que liga duas partes da borda do bambolê.
- COD (Diâmetro): O Diâmetro é uma corda muito especial! Ele é a maior corda que podemos traçar em uma circunferência, porque ele passa sempre pelo Centro (O) e liga dois pontos opostos da circunferência. Pensem que ele é como dois raios juntos, um de cada lado, que se encontram no centro. O diâmetro é sempre o dobro do raio!
Entendendo as Linhas e os Lugares
Para entender a geometria ainda melhor, precisamos conhecer três amigos muito importantes: o plano, a reta e o segmento de reta.
- Plano: Imaginem uma folha de papel bem grandona, que nunca acaba! Ou a superfície de uma mesa bem lisinha. Isso é um plano. É uma superfície plana, sem curvas, onde a gente pode desenhar e criar formas. Ele não tem começo nem fim!
- Reta: Pensem num fio de cabelo bem esticadinho, que vai para sempre, sem fazer curva. Isso é uma reta. Ela não tem começo nem fim, e é sempre retinha. Podemos desenhar retas em qualquer direção no plano.
- Segmento de Reta: Agora, se a gente pegar só um pedacinho desse fio de cabelo, com um começo e um fim, temos um segmento de reta. É como se a gente cortasse um pedaço da reta. O raio, a corda e o diâmetro que vimos na circunferência são exemplos de segmentos de reta!
Onde a Geometria Encontra os Números: Plano Cartesiano
Vocês sabiam que a gente pode dar “endereços” para os pontos no plano? Para isso, usamos o Plano Cartesiano!
Imaginem uma folha de caderno quadriculada. Agora, pensem em duas retas que se cruzam bem no meio, formando um “X” deitado e em pé.

- A reta que está “deitada” (horizontal) é o Eixo das Abscissas, ou Eixo X. Nela, marcamos os números para a direita (positivos) e para a esquerda (negativos).
- A reta que está “em pé” (vertical) é o Eixo das Ordenadas, ou Eixo Y. Nela, marcamos os números para cima (positivos) e para baixo (negativos).
Onde as duas retas se cruzam é o Ponto Zero ou Origem. Com esses dois eixos, podemos dar um “endereço” para qualquer ponto no plano, usando um par de números (X, Y). Isso é super útil para desenhar figuras com precisão!
O Que É “Lugar Geométrico”?
Essa frase pode parecer difícil, mas é bem legal! Lugar Geométrico é um conjunto de pontos que seguem uma mesma “regra” ou “condição”.
Por exemplo, a circunferência é um lugar geométrico! Qual é a regra? São todos os pontos que estão à mesma distância de um ponto central (o nosso Centro O). Legal, né?
Desenhando com o Compasso e a Régua!
Agora é a parte divertida! Vamos aprender a usar duas ferramentas muito importantes para desenhar circunferências e círculos: o compasso e a régua.

- Para usar o compasso:
- Peça ajuda a um adulto para ter certeza de que você sabe como manuseá-lo com segurança.
- Primeiro, marque um pontinho na sua folha. Esse será o Centro (O) da sua circunferência.
- Abra o compasso. A ponta seca (aquela que tem a agulhinha) será colocada no Centro (O).
- A ponta com o lápis vai girar em volta do Centro. A distância entre a ponta seca e a ponta do lápis será o seu Raio (R)!
- Com a ponta seca paradinha no centro, gire o compasso com cuidado, e voilà! Você terá desenhado uma linda circunferência!
- Para usar a régua: A régua nos ajuda a medir o raio e o diâmetro da nossa circunferência.
- Depois de desenhar sua circunferência, você pode usar a régua para medir o Raio (do Centro até a borda) ou o Diâmetro (passando pelo Centro, de uma borda à outra).
- A régua também é ótima para desenhar segmentos de reta, como as cordas!
Os Triângulos: Figuras de Três Lados!
Depois de explorar as formas redondas, vamos conhecer os triângulos! O próprio nome já diz: “tri” significa três, e “ângulo” é o “cantinho” da figura. Então, um triângulo é uma figura que tem três lados e três ângulos!
Imaginem uma fatia de pizza, um telhado de casa ou uma placa de trânsito em forma de “ceda”. São tudo triângulos!

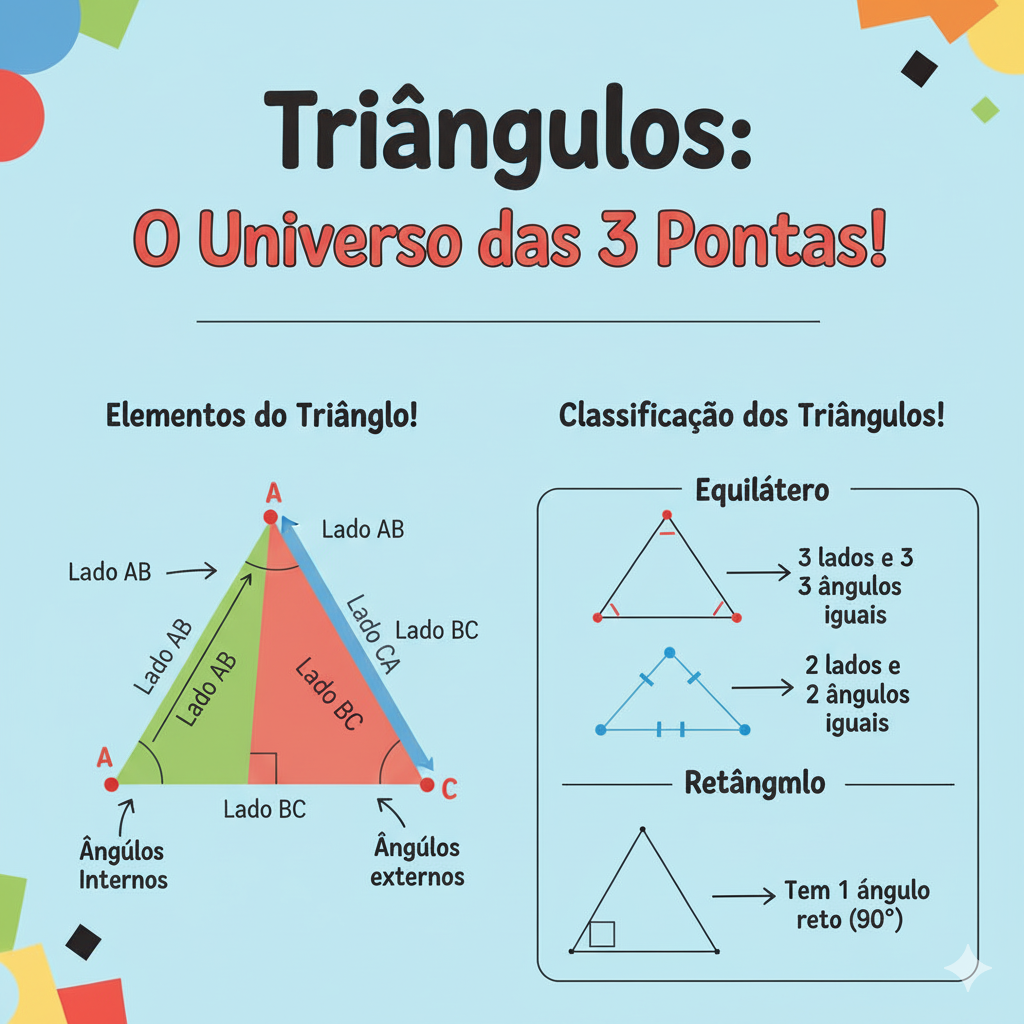
Propriedades dos Ângulos: Uma coisa mágica dos triângulos é que, se a gente somar a medida dos três ângulos de dentro (os ângulos internos), o resultado é SEMPRE 180 graus! Não importa o tamanho ou o formato do triângulo!
Classificação dos Triângulos: Cada Um Com Seu Jeito!
Os triângulos podem ser classificados de dois jeitos: pelos lados ou pelos ângulos.
Pelo Lado:
- Triângulo Equilátero: O nome já dá uma dica! “Equi” quer dizer igual. Então, o triângulo equilátero tem todos os três lados com a mesma medida. E, por causa disso, os três ângulos internos também são iguais (cada um medindo 60 graus)!

- Triângulo Isósceles: Esse triângulo é como se tivesse dois irmãos gêmeos! Ele tem dois lados com a mesma medida e, por consequência, os dois ângulos opostos a esses lados também são iguais.
- Triângulo Escaleno: Ah, o triângulo escaleno é o mais “diferentão”! Ele tem todos os três lados com medidas diferentes, e, claro, os três ângulos internos também são diferentes.
Pelos Ângulos:
- Triângulo Retângulo: Esse é muito famoso! O triângulo retângulo tem um ângulo reto, que mede exatamente 90 graus (é como o canto de uma parede ou de uma caixa). É por causa dele que existe o Teorema de Pitágoras, que vocês vão aprender quando crescerem mais um pouquinho!
- Triângulo Acutângulo: Todos os três ângulos internos são agudos, ou seja, menores que 90 graus.
- Triângulo Obtusângulo: Ele tem um ângulo obtuso, que é maior que 90 graus.
O Número Mágico: PI (π)!
Agora, preparem-se para conhecer uma das estrelas da matemática: o número PI, que é representado por uma letrinha grega muito charmosa, a π!
De onde ele vem? A história do Pi é fascinante! Há muito, muito tempo atrás, pessoas curiosas começaram a notar uma coisa interessante sobre as circunferências. Se você pegasse o comprimento da circunferência (ou seja, o tamanho da sua “borda”) e dividisse pelo tamanho do seu diâmetro (aquela linha que passa pelo centro), o resultado era sempre o mesmo número, não importa o tamanho da circunferência!
Esse número especial é o Pi (π)! Ele é aproximadamente 3,14159… e continua infinitamente, sem nunca repetir um padrão. É um número misterioso e muito útil!
- Comprimento da Circunferência: Pensem que vocês querem colocar uma fita em volta de um bambolê. O tamanho da fita será o comprimento da circunferência.
- Diâmetro da Circunferência: Já vimos que é a linha que passa pelo centro e liga dois pontos opostos da borda.
A razão (que em matemática significa uma divisão) entre o comprimento da circunferência e o diâmetro é sempre Pi (π)! Comprimento da Circunferência / Diâmetro = π
Isso significa que, para calcular o comprimento de qualquer circunferência, a gente pode usar a fórmula: Comprimento = π x Diâmetro Ou, como o diâmetro é duas vezes o raio (D = 2R), podemos escrever: Comprimento = 2 x π x Raio
O que é Perímetro?
Por último, vamos falar de perímetro. Perímetro é a medida do contorno de qualquer figura geométrica. Imaginem que vocês querem colocar uma cerca em volta do quintal da casa de vocês. O tamanho da cerca será o perímetro do quintal!
- Perímetro de Figuras Geométricas: Para calcular o perímetro de um triângulo, por exemplo, a gente soma a medida dos seus três lados. Se fosse um quadrado, somaríamos os quatro lados.
- Perímetro da Circunferência: Na circunferência, o perímetro é o próprio Comprimento da Circunferência, que acabamos de aprender que se calcula com o número Pi!
Que viagem incrível fizemos hoje pelo mundo da geometria, não é mesmo? Aprendemos sobre círculos e circunferências, seus elementos, triângulos com suas classificações, e até o número mágico Pi!
A geometria está em todo lugar, nos ajudando a entender as formas e o espaço ao nosso redor. Continuem curiosos e explorando esse universo fascinante da matemática!
Exercícios de Fixação e Desafios (Nível Iniciante)
Parte 1: Círculo e Circunferência
- Observando as Formas:
- Olhem ao redor de vocês. Encontrem 3 objetos que tenham a forma de uma circunferência (só o contorno). Desenhem ou listem esses objetos.
- Agora, encontrem 3 objetos que tenham a forma de um círculo (contorno preenchido). Desenhem ou listem esses objetos.
- Qual a principal diferença entre eles?
- Identificando os Elementos:
- No desenho de uma circunferência, marquem o Centro (O).
- Desenhem um Raio (R), saindo do centro até a borda.
- Desenhem um Diâmetro (D), passando pelo centro.
- Desenhem uma Corda (AB) que não passe pelo centro.
- Qual a relação entre o raio e o diâmetro? Se o raio mede 3 cm, quanto mede o diâmetro?
- Desenhando com o Compasso:
- Peguem seu compasso e sua régua.
- Desenhem uma circunferência com raio de 4 cm.
- Desenhem outra circunferência com diâmetro de 10 cm.
Parte 2: Triângulos
- Quantos Lados? Quantos Ângulos?
- O que um triângulo tem de especial no número de lados e de ângulos?
- Desenhem um triângulo qualquer e identifiquem seus vértices, lados e ângulos internos.
- Classificando Triângulos (pelos lados):
- Desenhem um triângulo equilátero (todos os lados iguais). Usem a régua para medir os lados.
- Desenhem um triângulo isósceles (dois lados iguais).
- Desenhem um triângulo escaleno (todos os lados diferentes).
- Classificando Triângulos (pelos ângulos):
- Desenhem um triângulo retângulo (com um ângulo de 90 graus). Pensem na quina de um livro para ajudar a fazer o ângulo reto.
Parte 3: O Número Pi e o Perímetro
- Onde mora o Pi?
- Qual é o número mágico que relaciona o comprimento de uma circunferência com seu diâmetro?
- Escrevam a fórmula para calcular o comprimento de uma circunferência usando o Pi (π) e o Diâmetro (D).
- Calculando o Perímetro:
- Se um bambolê tem um diâmetro de 80 cm, qual é o comprimento da sua circunferência (perímetro)? (Usem π ≈ 3,14)
- Se o raio de uma tampa de panela mede 15 cm, qual o comprimento da sua borda (perímetro)? (Usem π ≈ 3,14)
Desafio Extra:
- Em uma folha quadriculada, tentem desenhar um plano cartesiano. Marque os pontos (2, 3), (-1, 4), (3, -2) e (-2, -3). O que vocês observam sobre a localização deles?
Parabéns, exploradores da matemática! Vocês estão no caminho certo para desvendar todos os segredos das formas e dos números! Continuem praticando e se divertindo!


